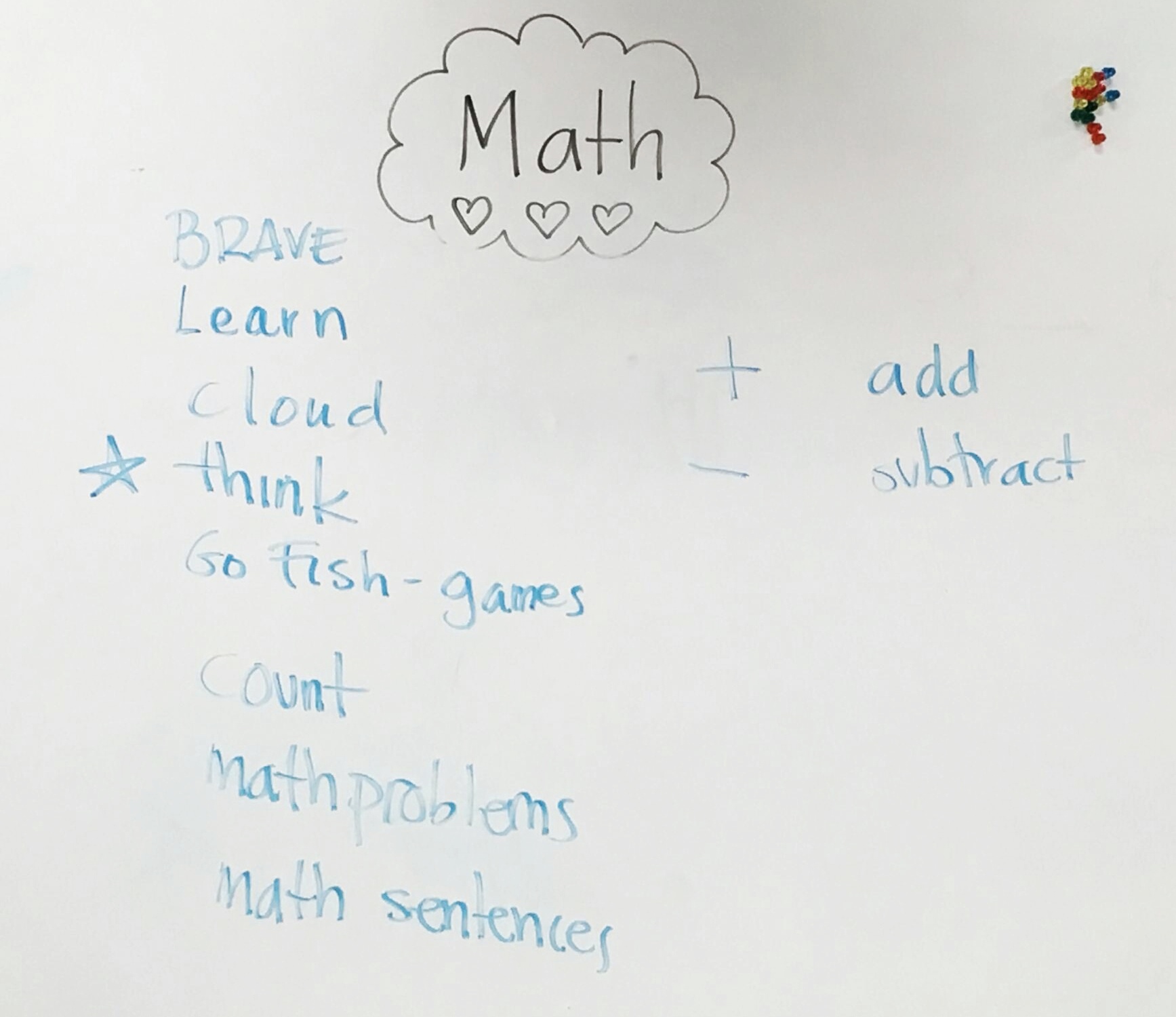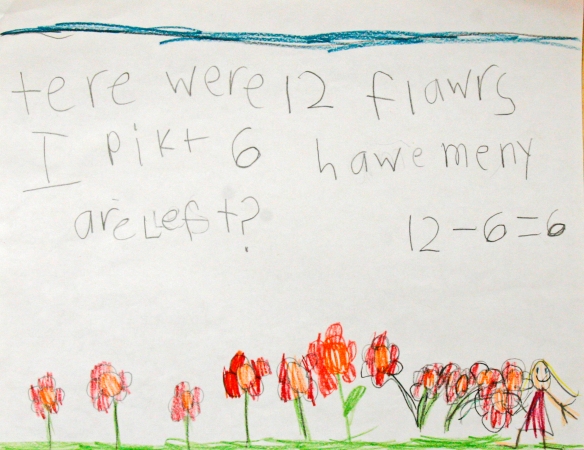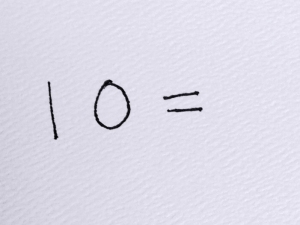We have fun-days in math each week. Usually they’re Fridays — because of the alliteration and the opportunity to wrap up the week with some small groups. But sometimes — when Friday Funday doesn’t work out, we start the next week with Monday Funday! Love the rhyming and joy it brings.
Our Fundays — be they Fridays or Mondays — do many things. They:
- allow my mighty mathematicians to engage with numbers and mathematical concepts and processes through play. This helps them grow in competence and confidence as they grow their math muscle and mindsets. (And remember, Play is Fun and Powerful!)
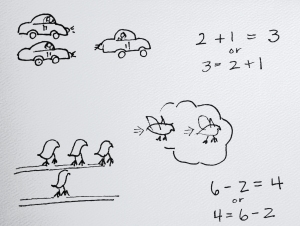
- provide opportunities for practicing things we are working on — +1, -1, counting, greater than and less than, partner numbers, counting on, shapes, patterns, and much more — by playing games.
- give choice and agency to the Kindergarten mathematicians. Sometimes they choose from a curated list of possibilities, other times the entire math center is fair game.
- give me the opportunity to work with small groups while the rest of the mathematicians are engaged in productive play.
Early in the year I added two types of paper to the math center. One has dots, the other has a grid of squares. I believe the squares are 1/2 inch squares and the dots are 1/2 inches away from each other. When I added the paper, I wasn’t sure what the Kindergarten mathematicians would do with it. I was purposeful in my choices — grids and dots of this size allow for many mathematical possibilities — but I didn’t have one specific thing that I wanted them to do. Instead I gave them something that might lead them towards mathematical play and exploration. For a while, no one used the papers. Then a few used the square grid paper to create patterns.
The Friday before our winter break this happened.

They used the dots to create patterns, and they used the grid to write numbers! Oh.my.gosh! ON THEIR OWN!!! I was super excited to see this. They were practicing writing and counting. They were noticing patterns, helping one another, using their current and prior knowledge to solve new problems, and teaching me more about what they know and don’t yet know. I gathered these papers and took the picture — at these two tables, with my feet in the photo — with intention! I wanted to document their work and emphasize their curiosity. And, I wanted to emphasize my own curiosity and interest in their work, thinking, understanding, and problem solving.
These mathematicians were psyched by the work they did, and the large numbers they were able to write. The one triumphantly reported that she had written to 1000! The other wanted to write more, but wasn’t sure how to write the numbers past 109. In both instances I acknowledged their amazing work and then entered into mathematical discourse with them.

We talked a bit about what they wrote, and how they decided to write it they way they did. We wondered if it were possible that 1000 would come so soon after 100. We noticed how the numbers preceding 110 were written. We talked about what made sense and why it made sense. We worked together to figure out the conventional way to write the numerals greater than 109. We ended the way we began — celebrating our thinking and work, acknowledging our big beautiful brains and awesome hearts, honoring our courage, might, and joy as mathematicians.